Inhalt
… besonders wenn sie die Zukunft betreffen
Was macht die eigentlich die universelle Faszination des Phänomens „Börse“ aus? Sicher, beim Aktienhandel schwingt auch immer ein wenig der Traum vom existenzdruckfreien Leben mit. Doch mindestens ebenso schwer dürfte ein andere Faktor wiegen: Der Kontrast zwischen Ordnung und Chaos. Betrachten wir hierzu die Börse aus systemtheoretischer Sicht: Eine überschaubare Anzahl von Elementen, sprich handelbaren Wertpapieren, und simpler Interaktionsregeln, in Menge und Preis fixierte Order, entfalten ein hochkomplexes Ursache-Wirkungs-Geflecht. Dieses verdichtete sich wiederum laufend in einer einzigen dynamischen Größe, dem Kurs. Faszinierend, nicht wahr?
Wie bei jeder anderen sozialen Ordnung auch handelt es sich bei der Börse um ein kybernetisches System. Kybernetische Systeme zeichnen sich dabei durch zwei wesentliche Faktoren aus. Zum einen durch Nichtlinearität, also der nichtproportionalen Änderung von Systemgrößen im Zeitverlauf. Zum anderen durch Rückkopplungen, den Einfluss vergangener auf zukünftige Systemänderungen. Beide Faktoren spiegeln sich plastisch in der Kursentwicklung von Wertpapieren wider: Diese verlaufen einerseits meist alles andere als kontinuierlich, andererseits wirken sich Änderungen unmittelbar auf nachfolgende Handelsorder und damit die nächste Kursstellung aus.
Auf Mustersuche in Kursverläufen
Soziale Ordnungen sind zudem in der Regel abzählbar unendlichen Einflussfaktoren ausgesetzt. Auch dies ist ein für die Börse typisches Charakteristikum. Nicht zuletzt deswegen existiert eine Form der Finanzanalyse, die einzig und allein auf Basis der Kurshistorie versucht, geeignete Ein- und Ausstiegszeitpunkte zu ermitteln beziehungsweise die künftige Kursentwicklung vorherzusagen. Vertreter der sogenannten Technischen Analyse stützen sich dabei fast ausschließlich auf Diagramme mit der graphischen Aufbereitung von Zeitreihen, kurz Charts.
Aus Charts versuchen Analysten Formationen wie Untertassen, Dreiecke, Mehrfachhochs und Mehrfachtiefs, Schulter-Kopf-Schulter-Formationen, Flaggen, Keile und Wimpel sowie Trendfolgeindikatoren, Oszillatoren, Kanäle und Linien herauszulesen. Aus diesen Mustern leiten Charttechniker schließlich künftige Preistrends ab. Mit ihrem Instrumentarium bilden sie dann auch das exakte Gegenstück zu den Fundamentalanalysten.
Die Chartanalytiker auf Zufallspfaden
Die Charttechnik basiert auf der richtigen Erkenntnis, dass die Erfassung sämtlicher Ursache-Wirkungs-Beziehungen lediglich innerhalb einfacher Strukturen in begrenztem Maße leistbar, in kybernetischen Systemen jedoch unmöglich ist. Von daher verzichten sie konsequenterweise auf jede Erhebung fundamentaler Daten oder Kennzahlen und konzentrieren sich allein auf die alle Einflüsse widerspiegelnden Kursmuster. Immerhin macht sich die Chartanalyse mit ihrem Versuch, künftige Kurse auf Basis vergangener Kurse vorherzusagen, die beiden tragenden Säulen kybernetischer Systeme, die Rückbezüglichkeit sowie die Nichtlinearität, zu Eigen.
Burton Malkiel, emeritierter Professor für Volkswirtschaftslehre der Princeton Universität hat in „A Random Walk Down Wallstreet“, in Deutschland unter dem Titl „Börsenerfolg ist (k)ein Zufall“ (*) veröffentlicht und mittlerweile ein Klassiker der Finanzliteratur, das Ergebnis dutzender Studien zur Aussagekraft der Charttechnik zusammengefasst. Wie alle anderen Prognosemodelle auch siedelt sie sich statistisch betrachtet im Reich des Zufalls an. Das kann auch gar nicht anders sein, liegt dem Phänomen der Kursbildung an Börsen doch ein grundsätzliches Vorhersageproblem zu Grunde. Dies soll nachfolgend anhand eines einfachen Modells erläutert werden, wobei wir um ein wenig Mathematik nicht umhinkommen.
Eine Weltformel im Praxistest
Angenommen, es gelänge einem Analysten den historischen Verlauf der zyklischen Extremwerte, also der Kursmaxima und -minima über die Formel Kt+1 = E * Kt * (1 – Kt) abzubilden. (K) steht dabei für den Kurs beziehungsweise Trend des Wertpapiers oder Index, (t) bezeichnet die jeweilige Periode, zum Beispiel ein Quartal, (E) schließlich fasst sämtliche Einflussgrößen auf die Kursentwicklung zusammen. Nach dieser Formel errechnet sich der Kurstrend (K) des folgenden Quartals (t+1) aus der Multiplikation der Einflussgrößen (E) mit dem Kurstrend des aktuellen Quartals (t).
Die Formel wahrt sowohl das Prinzip der Rückbezüglichkeit als auch der Nichtlinearität, das heißt einerseits hängt der künftige Kurs vom aktuellen Kurs ab, andererseits weist der Kursverlauf keinen stetigen Verlauf auf. Für (E) ermittelt der Analyst exemplarisch den Faktor 3,9. Berechnet er nun mit Hilfe einer Tabellenkalkulation die Werte der Formel über 100 Iterationen respektive Perioden und lässt diese auf einem Liniendiagramm abtragen, ergibt sich ein asymmetrisch oszillierender Verlauf abwechselnder Kursmaxima und -minima:
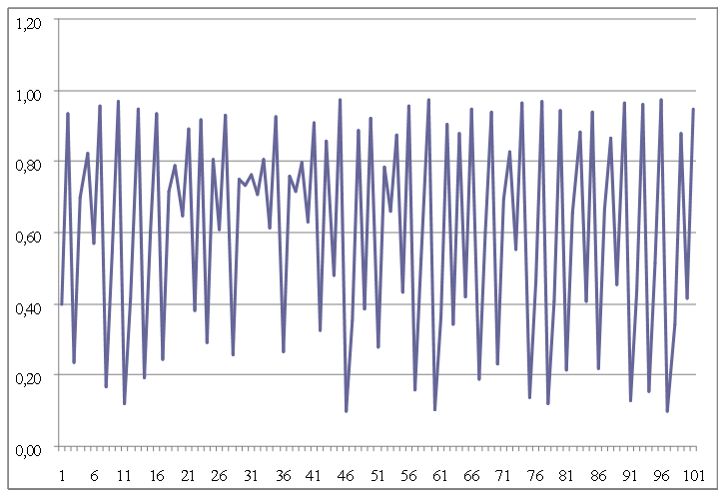
Allerdings ist bei genauerer Betrachtung ein interessantes Phänomen zu beobachten: Die Formel einschließlich sämtlicher Varianten liefert letztendlich nichts anderes als Chaoszustände. Ursächlich hierfür ist (E), also die Summe der externen Einflussgrößen. Kleinste Veränderungen führen hierbei zu dramatischen Abweichungen im Kursverlauf, wie beispielsweise eine Änderung von 3,9 auf 3,90001 eindrucksvoll demonstriert. Im direkten Vergleich entwickeln sich beide Kurven zunächst weitgehend parallel, um im Zeitverlauf – konkret ab der 18. Iteration – völlig unterschiedliche Verläufe zu nehmen:
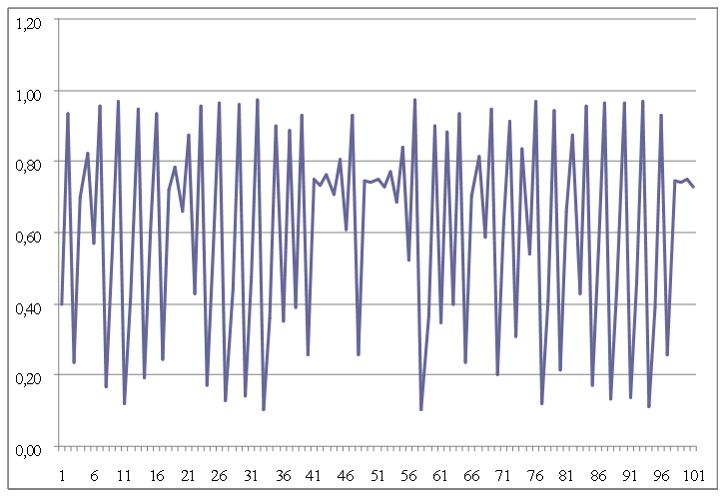
Im Reich des Chaos
Dieses analytische Dilemma würde übrigens selbst dann bestehen bleiben, wenn (E) exakt bestimmt werden könnte. Rückkopplung und Nichtlinearität können selbst bei identischen Ausgangswerten zu unterschiedlichen Verläufen führen, die sich mathematisch nicht berechnen lassen. Das liegt daran, dass bereits die einfache obige Formel nach wenigen Dutzend Iterationen die Rechengenauigkeit jeder Tabellenkalkulation sprengt.
Da so Rundungen und damit Ungenauigkeiten unausweichlich sind, ist es prinzipiell nicht möglich, die Entwicklung selbst eines festen Gesetzmäßigkeiten unterliegenden kybernetischen Systems über einen hinreichend langen Zeitraum vorherzusagen. Mit jeder Zeiteinheit, um die dieser ausgedehnt wird nimmt die dafür nötige Rechengenauigkeit exponentiell zu und stößt rasch in Dimensionen vor, für welche selbst eine hypothetische Nutzung der globalen Rechnerkapazitäten nicht ausreichen würde.
Im Ergebnis sind rückgekoppelte nichtlineare Systeme wie die Börse geradezu durch Chaoszustände gekennzeichnet. Kursentwicklungen sind daher ebenso unmöglich zu prognostizieren wie Geschichts- oder Klimaverläufe, völlig unabhängig von der Qualität der zugrunde liegenden Theorien und Modelle. Unauffällige Änderungen von (E) können dabei zu unvorhersehbaren Konvergenzen führen, etwa zu vertikalen Exzessen oder Abstürzen gen Nullwert; letzteres lässt sich recht eindrucksvoll demonstrieren, indem (E) der Wert 4,09 zugewiesen wird:
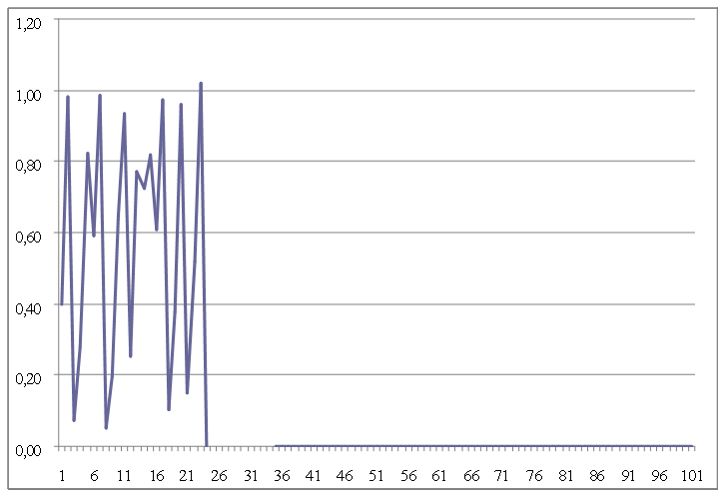
Isaac Newtons späte Erkenntnis
Doch warum bleibt den Sozialwissenschaften verwehrt, was bei den Naturwissenschaften so gut funktioniert? Eine erste Ahnung überkam das Universalgenie Sir Isaac Newton nach einer kapitalen Fehlspekulation. Nachdem er 20.000 Pfund – heute entspräche das einem Millionenvermögen – beim sogenannten Südseeschwindel, englisch „South Sea Bubble“, von 1720 verlorenen hatte resümierte er zutreffend: „Ich kann zwar die Bewegungen der Himmelskörper berechnen, aber nicht die Verrücktheit der Menschen.“
Der visionäre Engländer erkannte sehr richtig, dass es zwischen der Theoriebildung in der naturwissenschaftlichen Sphäre einerseits und der sozialwissenschaftlichen Sphäre andererseits einen fundamentalen Unterschied gibt: Die eine stützt sich auf die Analyse von Objekten, die andere auf die von Subjekten. Letztere, sprich Menschen, sind aber im Gegensatz zu Dingen nicht zur tatenlosen Passivität verdammt, sondern jederzeit in der Lage zu handeln, aktiv auf die Umwelt und damit andere Subjekte einzuwirken oder zu reagieren. Und das schließt sämtliche sie betreffende Theorien mit ein. Als Subjekte sind sie jederzeit in der Lage, diese durch ihr Verhalten zu bestätigen oder zu widerlegen.
Diese Erkenntnis war auch einer der Gründe, warum ich bei meiner persönlichen Anlagestrategie eine Kehrtwende vom Kursgewinn- zum Einkommensinvestor vollzogen habe.
PS: Die „Weltformel“ beziehungsweise das Rechenbeispiel ist einem Text des leider viel zu früh verstorbenen Wirtschaftsdozenten Harald Zingel entlehnt.
Anzeige
Beitrag teilen
Fragen und Anmerkungen
Sie haben noch Fragen zur Systemtheorie oder Anmerkungen zu den Inhalten dieses Beitrags? Dann schreiben Sie mir doch – egal ob mit oder ohne E-Mail-Adresse!




Hallo Hr. Pazos,
für Charttechniken habe ich mich bisher nie interessiert, da sie für mich persönlich Kaffeesatzleserei sind. Trotzdem möchte ich aufgeschlossen bleiben und ggf. etwas dazu lernen. So habe ich mich durch den Blogbeitrag „gequält“ und so hat sich meine persönliche Erkenntnis bestätigt: ich bleibe meiner Strategie treu und bleibe „Highyield-bye and hold-Investor
beste Grüße Hans-Jürgen
Hallo Hans-Jürgen,
Charts sind Aufzeichnungen historischer Wertpapierkurse und haben damit ausschließlich einen geschichtlichen Wert. Aber ebensowenig, wie aus vergangenen Geschichtsverläufen Prognosen über künftige Geschichtsverläufe möglich sind, können Kursentwicklungen verlässlich aus Charts vorhergesagt werden. Wer tiefer in das Thema einsteigen möchte, dem empfehle ich „Das Elend des Historizismus“ von Karl Popper.
Beste Grüße
Luis
Die einzige mathematische Theorie, die in der Lage ist, Kursverläufe zu beschreiben, ist meines Wissens die fraktale Geometrie Mandelbrots. Sie kommt mit den Kursmustern klar, die auf verschiedenen Zeitebenen sichtbar sind und den Trends, Crashs und Booms, also turbulenten Effekten. Siehe dazu sein Buch „Fraktale und Finanzen“, das ich auf meinem Blog in 2 Teilen ausführlich besprochen habe: https://www.covacoro.de/2016/08/12/buchreview-fraktale-und-finanzen-teil-2/
Beschreiben, also analysieren und synthesieren, heißt aber nicht, dass man Kurse prognostizieren könnte. Wohl aus diesem Grund findet Mandelbrots Werk wenig Beachtung, während vereinfachende Modelle und Theorien sogar mit dem Nobelpreis geehrt werden, siehe Markteffizienzhypothese.
Danke für die Ergänzung. Das Buch habe ich auch gelesen und kann es ebenfalls empfehlen. Der wichtigste Hinweis zu mathematischen Modellen steht im vorletzten Satz: Synthetisieren ja, prognostizieren nein!